2024-10-13 16:58:10 红河华图考试网 http://honghe.huatu.com/ 文章来源:云南华图

1、【答案】A
【解析】
第一步,本题考查排列组合问题。
第二步,要求恰好满足学分,即选修4分。分情况讨论:
(1)选修两门2分选修课,情况数为:![]() =3(种);
=3(种);
(2)选修一门2分和两门1分选修课,情况数为:![]() =18(种);
=18(种);
(3)选修四门1分选修课,情况数为![]() =1(种)。
=1(种)。
则总情况数为3+18+1=22(种)。
因此,选择A选项。
2、【答案】A
【解析】
第一步,本题考查不定方程问题,用代入排除法解不定方程。
第二步,设获得一等奖的有x位选手、获得二等奖的有y位选手、获得三等奖的有z位选手。根据共15位选手参赛和总分为72分,可列不定方程组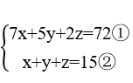 ,①-②×5可得:2x-3z=-3。
,①-②×5可得:2x-3z=-3。
第三步,问最多有几位选手获得一等奖,最值代入,优先代入D选项,x=7,z无整数解,排除;代入A选项,若x=6,z=5,y=4,满足题意。
因此,选择A选项。
3、【答案】D
【解析】
第一步,本题考查约数倍数问题。
第二步,排练总人数应为4、6、7的公倍数,最小为84,不到一百人即84人。84人中女性为(84+10)÷2=47人,超过20岁的有(84-20)÷2=32人。让女性与超过20岁尽量无重叠,则最多有47+32=79人,此时不超过20岁的男性最少,为84-79=5人。
因此,选择D选项。
4、【答案】B
【解析】
第一步,本题考查基础计算,属于循环周期类问题。
第二步,根据从1到3依次不重复地报数,可知每报数3次,会有1人下池游泳。
第三步,仅剩1名运动员尚未下池游泳时,可知已下池游泳的人数为30-1=29(人),则需报数29×3=87(人次)。
因此,选择B选项。
5、【答案】B
【解析】
第一步,本题考查不定方程问题。
第二步,假设x人获得一等奖金,y人获得二等奖金,z人获得三等奖金,根据题意可列方程:①x+y+z=11;②3000x+2000y+500z=15000。化简②式得到③6x+4y+z=30。6×①-③可得:2y+5z=36,36和2y为偶数,则5z为偶数,故z为偶数,排除A、C选项。代入B选项,若z=6,则y=3,x=11-6-3=2,满足题意。(若代入D选项,z=8,则y为负数,不合题意,排除)
因此,选择B选项。
(编辑:xufurong)上一篇:红河2025年事业单位联考笔试练习题+答案解析(10月11日)
下一篇:没有了